线性代数
numpy 和 scipy 中,负责进行线性代数部分计算的模块叫做 linalg。
import numpy as np
import numpy.linalg
import scipy as sp
import scipy.linalg
import matplotlib.pyplot as plt
from scipy import linalg
%matplotlib inlinenumpy.linalg VS scipy.linalg
一方面scipy.linalg 包含 numpy.linalg 中的所有函数,同时还包含了很多 numpy.linalg 中没有的函数。
另一方面,scipy.linalg 能够保证这些函数使用 BLAS/LAPACK 加速,而 numpy.linalg 中这些加速是可选的。
因此,在使用时,我们一般使用 scipy.linalg 而不是 numpy.linalg。
我们可以简单看看两个模块的差异:
print "number of items in numpy.linalg:", len(dir(numpy.linalg))
print "number of items in scipy.linalg:", len(dir(scipy.linalg))number of items in numpy.linalg: 36
number of items in scipy.linalg: 115numpy.matrix VS 2D numpy.ndarray
线性代数的基本操作对象是矩阵,而矩阵的表示方法主要有两种:numpy.matrix 和 2D numpy.ndarray。
numpy.matrix
numpy.matrix 是一个矩阵类,提供了一些方便的矩阵操作:
- 支持类似
MATLAB创建矩阵的语法 - 矩阵乘法默认用
*号 .I表示逆,.T表示转置
可以用 mat 或者 matrix 来产生矩阵:
A = np.mat("[1, 2; 3, 4]")
print repr(A)
A = np.matrix("[1, 2; 3, 4]")
print repr(A)matrix([[1, 2],
[3, 4]])
matrix([[1, 2],
[3, 4]])转置和逆:
print repr(A.I)
print repr(A.T)matrix([[-2. , 1. ],
[ 1.5, -0.5]])
matrix([[1, 3],
[2, 4]])矩阵乘法:
b = np.mat('[5; 6]')
print repr(A * b)matrix([[17],
[39]])2 维 numpy.ndarray
虽然 numpy.matrix 有着上面的好处,但是一般不建议使用,而是用 2 维 numpy.ndarray 对象替代,这样可以避免一些不必要的困惑。
我们可以使用 array 复现上面的操作:
A = np.array([[1,2], [3,4]])
print repr(A)array([[1, 2],
[3, 4]])逆和转置:
print repr(linalg.inv(A))
print repr(A.T)array([[-2. , 1. ],
[ 1.5, -0.5]])
array([[1, 3],
[2, 4]])矩阵乘法:
b = np.array([5, 6])
print repr(A.dot(b))array([17, 39])普通乘法:
print repr(A * b)array([[ 5, 12],
[15, 24]])scipy.linalg 的操作可以作用到两种类型的对象上,没有区别。
基本操作
求逆
矩阵 $\mathbf{A}$ 的逆 $\mathbf{B}$ 满足:$\mathbf{BA}=\mathbf{AB}=I$,记作 $\mathbf{B} = \mathbf{A}^{-1}$。
事实上,我们已经见过求逆的操作,linalg.inv 可以求一个可逆矩阵的逆:
A = np.array([[1,2],[3,4]])
print linalg.inv(A)
print A.dot(scipy.linalg.inv(A))[[-2. 1. ]
[ 1.5 -0.5]]
[[ 1.00000000e+00 0.00000000e+00]
[ 8.88178420e-16 1.00000000e+00]]求解线性方程组
例如,下列方程组
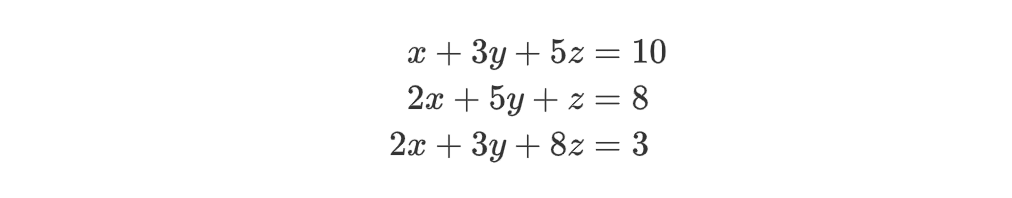
的解为:
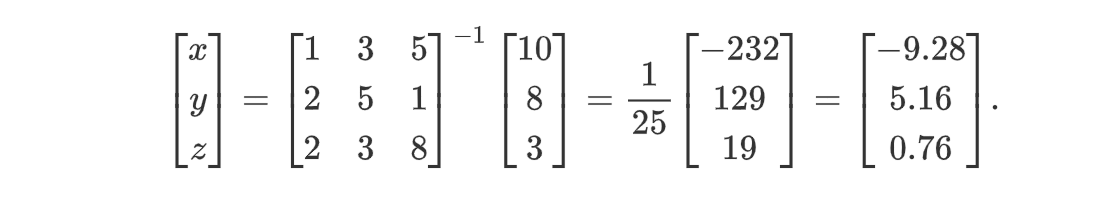
我们可以使用 linalg.solve 求解方程组,也可以先求逆再相乘,两者中 solve 比较快。
import time
A = np.array([[1, 3, 5],
[2, 5, 1],
[2, 3, 8]])
b = np.array([10, 8, 3])
tic = time.time()
for i in xrange(1000):
x = linalg.inv(A).dot(b)
print x
print A.dot(x)-b
print "inv and dot: {} s".format(time.time() - tic)
tic = time.time()
for i in xrange(1000):
x = linalg.solve(A, b)
print x
print A.dot(x)-b
print "solve: {} s".format(time.time() - tic)[-9.28 5.16 0.76]
[ 0.00000000e+00 -1.77635684e-15 -8.88178420e-16]
inv and dot: 0.0353579521179 s
[-9.28 5.16 0.76]
[ 0.00000000e+00 -1.77635684e-15 -1.77635684e-15]
solve: 0.0284671783447 s计算行列式
方阵的行列式为
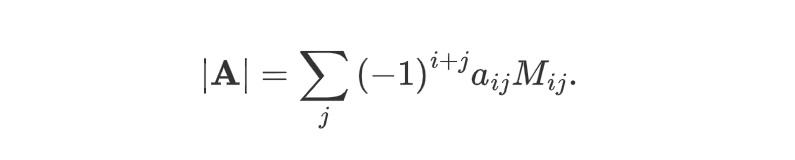
其中 $a{ij}$ 表示 $\mathbf{A}$ 的第 $i$ 行 第 $j$ 列的元素,$M{ij}$ 表示矩阵 $\mathbf{A}$ 去掉第 $i$ 行 第 $j$ 列的新矩阵的行列式。
例如,矩阵

的行列式是:
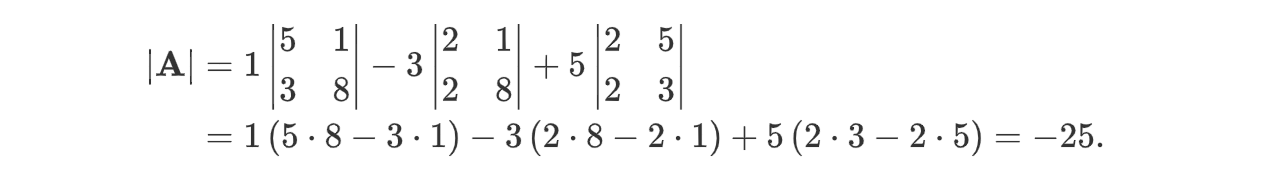
可以用 linalg.det 计算行列式:
A = np.array([[1, 3, 5],
[2, 5, 1],
[2, 3, 8]])
print linalg.det(A)-25.0计算矩阵或向量的模
矩阵的模定义如下:
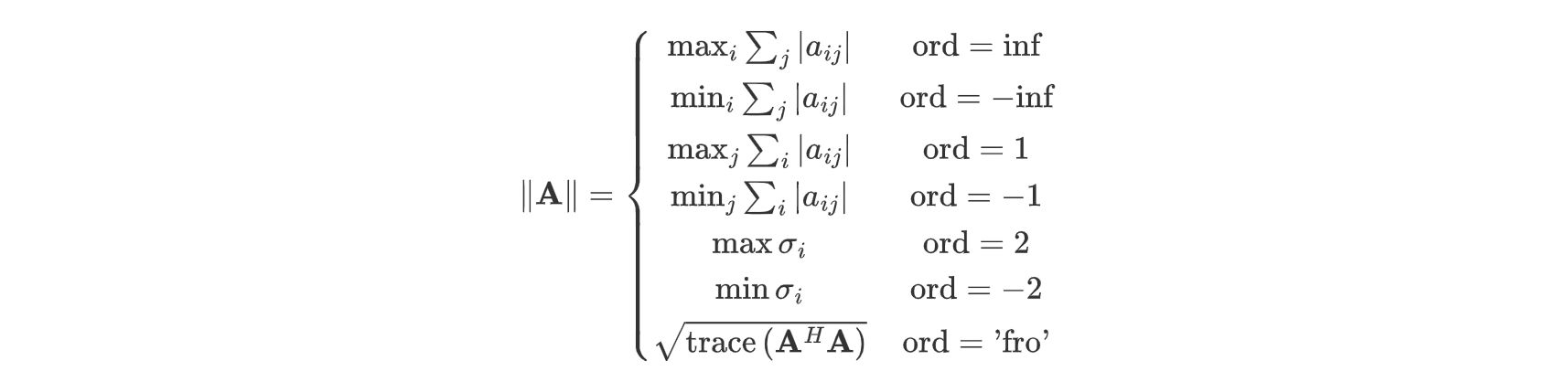
其中,$\sigma_i$ 是矩阵的奇异值。
向量的模定义如下:
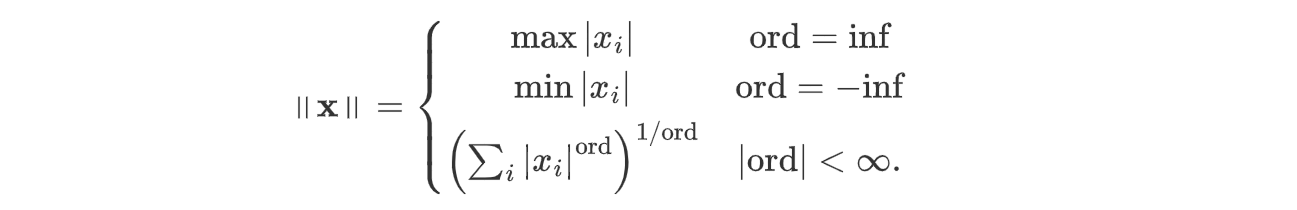
linalg.norm 可以计算向量或者矩阵的模:
A = np.array([[1, 2],
[3, 4]])
print linalg.norm(A)
print linalg.norm(A,'fro') # frobenius norm 默认值
print linalg.norm(A,1) # L1 norm 最大列和
print linalg.norm(A,-1) # L -1 norm 最小列和
print linalg.norm(A,np.inf) # L inf norm 最大行和5.47722557505
5.47722557505
6
4
7最小二乘解和伪逆
问题描述
所谓最小二乘问题的定义如下:
假设 $y_i$ 与 $\mathbf{x_i}$ 的关系可以用一组系数 $c_j$ 和对应的模型函数 $f_j(\mathbf{x_i})$ 的模型表示:
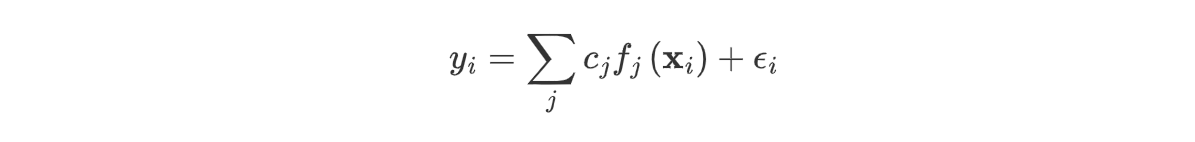
其中 $\epsilon_i$ 表示数据的不确定性。最小二乘就是要优化这样一个关于 $c_j$ 的问题:
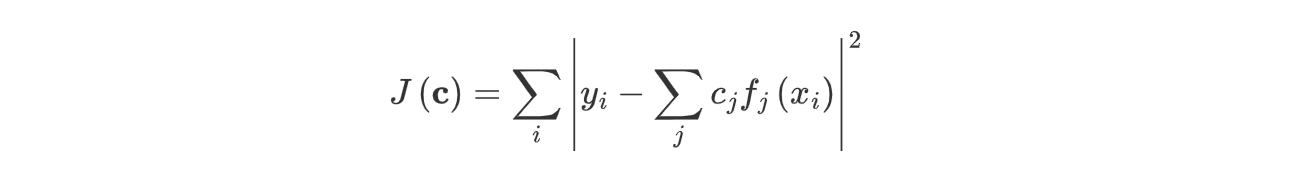
其理论解满足:
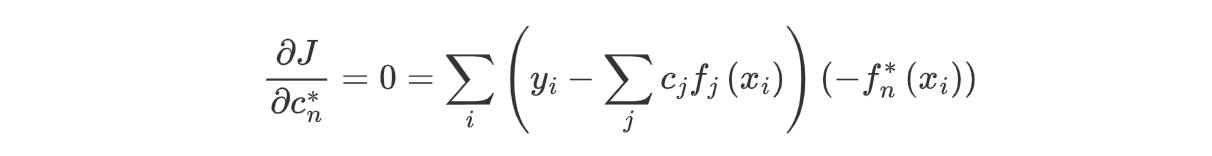
改写为:

其中:
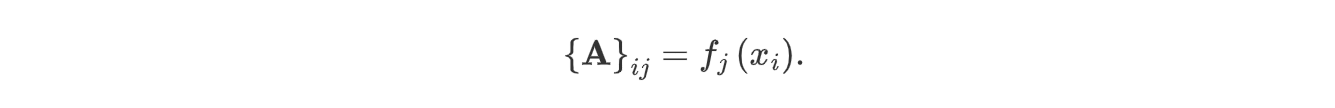
当 $\mathbf{A^HA}$ 可逆时,我们有:
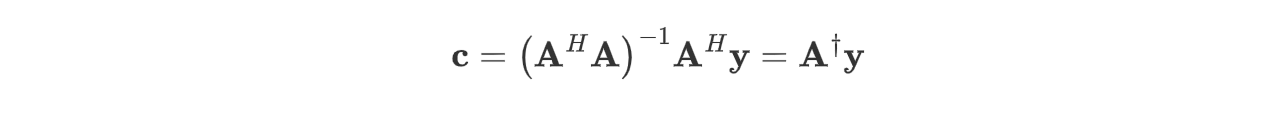
矩阵 $\mathbf{A}^{\dagger}$ 叫做 $\mathbf{A}$ 的伪逆。
问题求解
注意到,我们的模型可以写为:
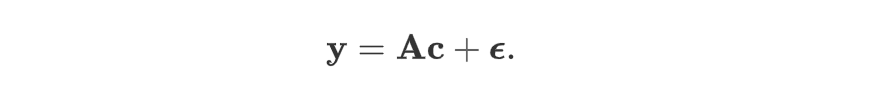
在给定 $\mathbf{y}$ 和 $\mathbf{A}$ 的情况下,我们可以使用 linalg.lstsq 求解 $\mathbf c$。
在给定 $\mathbf{A}$ 的情况下,我们可以使用 linalg.pinv 或者 linalg.pinv2 求解 $\mathbf{A}^{\dagger}$。
例子
假设我们的数据满足:
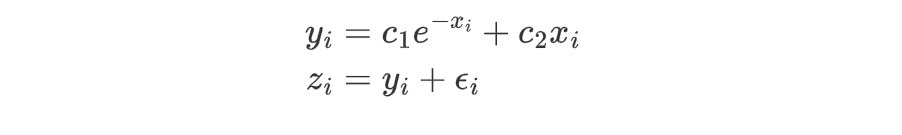
其中 $x_i = \frac{i}{10},\ i = 1,\dots,10$,$c_1 = 5, c_2 = 2$,产生数据
c1, c2 = 5.0, 2.0
i = np.r_[1:11]
xi = 0.1*i
yi = c1*np.exp(-xi) + c2*xi
zi = yi + 0.05 * np.max(yi) * np.random.randn(len(yi))构造矩阵 $\mathbf A$:
A = np.c_[np.exp(-xi)[:, np.newaxis], xi[:, np.newaxis]]
print A[[ 0.90483742 0.1 ]
[ 0.81873075 0.2 ]
[ 0.74081822 0.3 ]
[ 0.67032005 0.4 ]
[ 0.60653066 0.5 ]
[ 0.54881164 0.6 ]
[ 0.4965853 0.7 ]
[ 0.44932896 0.8 ]
[ 0.40656966 0.9 ]
[ 0.36787944 1. ]]求解最小二乘问题:
c, resid, rank, sigma = linalg.lstsq(A, zi)
print c[ 4.87016856 2.19081311]其中 c 的形状与 zi 一致,为最小二乘解,resid 为 zi - A c 每一列差值的二范数,rank 为矩阵 A 的秩,sigma 为矩阵 A 的奇异值。
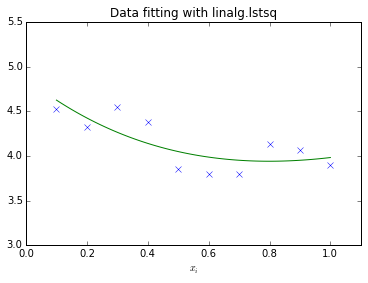
查看拟合效果:
xi2 = np.r_[0.1:1.0:100j]
yi2 = c[0]*np.exp(-xi2) + c[1]*xi2
plt.plot(xi,zi,'x',xi2,yi2)
plt.axis([0,1.1,3.0,5.5])
plt.xlabel('$x_i$')
plt.title('Data fitting with linalg.lstsq')
plt.show()
广义逆
linalg.pinv 或 linalg.pinv2 可以用来求广义逆,其区别在于前者使用求最小二乘解的算法,后者使用求奇异值的算法求解。
矩阵分解
特征值和特征向量
问题描述
对于给定的 $N \times N$ 矩阵 $\mathbf A$,特征值和特征向量问题相当与寻找标量 $\lambda$ 和对应的向量 $\mathbf v$ 使得:
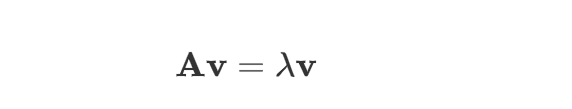
矩阵的 $N$ 个特征值(可能相同)可以通过计算特征方程的根得到:
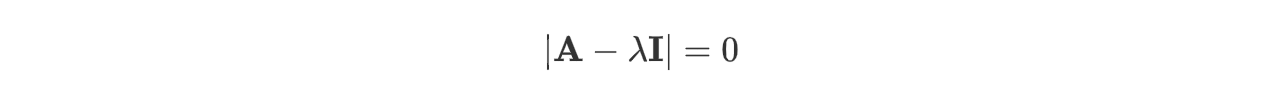
然后利用这些特征值求(归一化的)特征向量。
问题求解
linalg.eig(A)- 返回矩阵的特征值与特征向量
linalg.eigvals(A)- 返回矩阵的特征值
linalg.eig(A, B)- 求解 $\mathbf{Av} = \lambda\mathbf{Bv}$ 的问题
例子
矩阵为

特征多项式为:
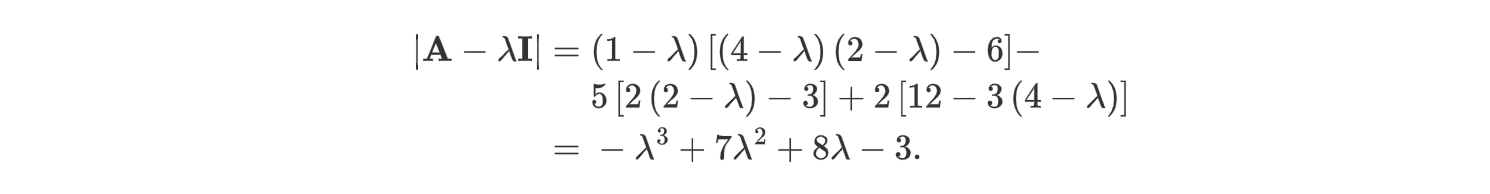
特征根为:
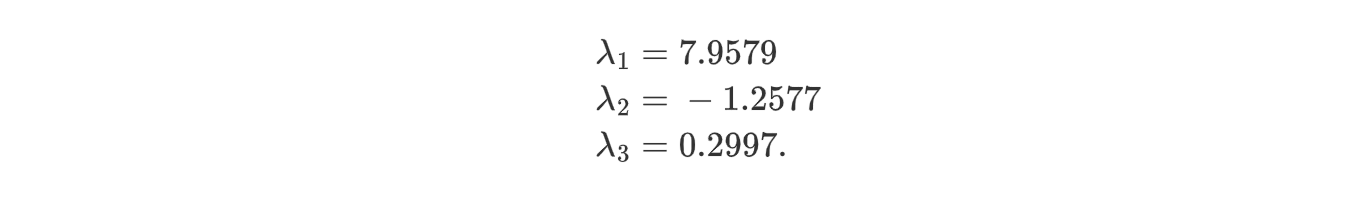
A = np.array([[1, 5, 2],
[2, 4, 1],
[3, 6, 2]])
la, v = linalg.eig(A)
print la
# 验证是否归一化
print np.sum(abs(v**2),axis=0)
# 第一个特征值
l1 = la[0]
# 对应的特征向量
v1 = v[:, 0].T
# 验证是否为特征值和特征向量对
print linalg.norm(A.dot(v1)-l1*v1)[ 7.95791620+0.j -1.25766471+0.j 0.29974850+0.j]
[ 1. 1. 1.]
3.23301824835e-15奇异值分解
问题描述
$M \times N$ 矩阵 $\mathbf A$ 的奇异值分解为:
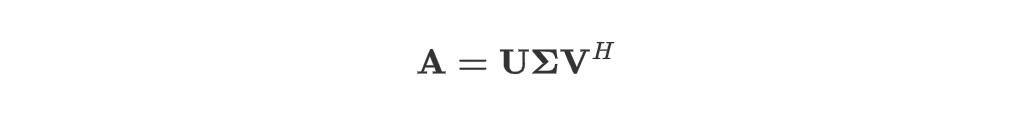
其中 $\boldsymbol{\Sigma}, (M \times N)$ 只有对角线上的元素不为 0,$\mathbf U, (M \times M)$ 和 $\mathbf V, (N \times N)$ 为正交矩阵。
其具体原理可以查看维基百科:
https://en.wikipedia.org/wiki/Singular_value_decomposition
问题求解
U,s,Vh = linalg.svd(A)- 返回 $U$ 矩阵,奇异值 $s$,$V^H$ 矩阵
Sig = linalg.diagsvd(s,M,N)- 从奇异值恢复 $\boldsymbol{\Sigma}$ 矩阵
例子
奇异值分解:
A = np.array([[1,2,3],[4,5,6]])
U, s, Vh = linalg.svd(A)$\boldsymbol{\Sigma}$ 矩阵:
M, N = A.shape
Sig = linalg.diagsvd(s,M,N)
print Sig[[ 9.508032 0. 0. ]
[ 0. 0.77286964 0. ]]检查正确性:
print A
print U.dot(Sig.dot(Vh))[[1 2 3]
[4 5 6]]
[[ 1. 2. 3.]
[ 4. 5. 6.]]LU 分解
$M \times N$ 矩阵 $\mathbf A$ 的 LU 分解为:

$\mathbf P$ 是 $M \times M$ 的单位矩阵的一个排列,$\mathbf L$ 是下三角阵,$\mathbf U$ 是上三角阵。
可以使用 linalg.lu 进行 LU 分解的求解:
具体原理可以查看维基百科:
https://en.wikipedia.org/wiki/LU_decomposition
A = np.array([[1,2,3],[4,5,6]])
P, L, U = linalg.lu(A)
print P
print L
print U
print P.dot(L).dot(U)[[ 0. 1.]
[ 1. 0.]]
[[ 1. 0. ]
[ 0.25 1. ]]
[[ 4. 5. 6. ]
[ 0. 0.75 1.5 ]]
[[ 1. 2. 3.]
[ 4. 5. 6.]]Cholesky 分解
Cholesky 分解是一种特殊的 LU 分解,此时要求 $\mathbf A$ 为 Hermitian 正定矩阵 ($\mathbf A = \mathbf{A^H}$)。
此时有:
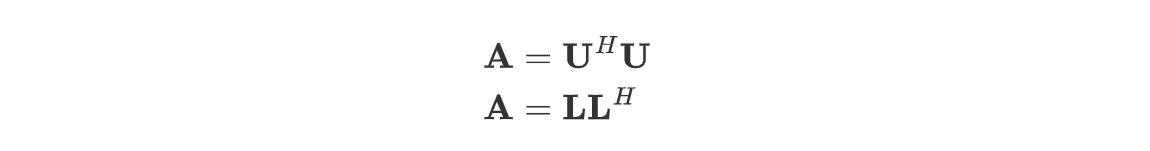
即
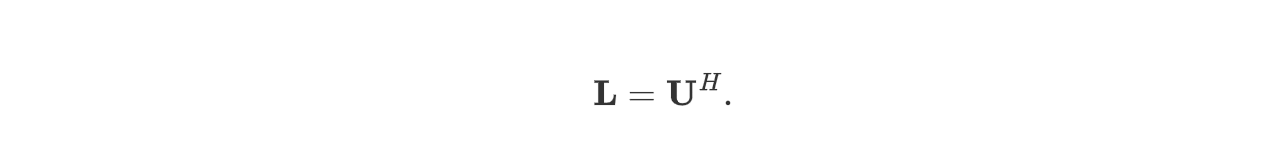
可以用 linalg.cholesky 求解。
QR 分解
$M×N$ 矩阵 $\mathbf A$ 的 QR 分解为:
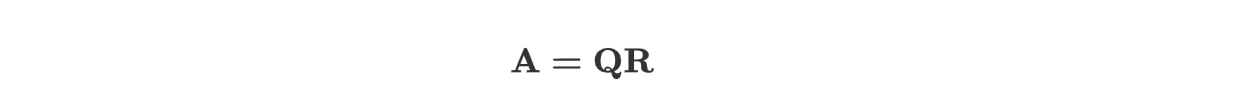
$\mathbf R$ 为上三角形矩阵,$\mathbf Q$ 是正交矩阵。
维基链接:
https://en.wikipedia.org/wiki/QR_decomposition
可以用 linalg.qr 求解。
Schur 分解
对于 $N\times N$ 方阵 $\mathbf A$, Schur 分解要求找到满足下式的矩阵:
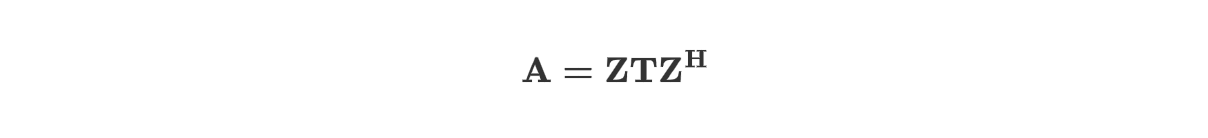
其中 $\mathbf Z$ 是正交矩阵,$\mathbf T$ 是一个上三角矩阵。
维基链接:
https://en.wikipedia.org/wiki/Schur_decomposition
A = np.mat('[1 3 2; 1 4 5; 2 3 6]')
print A
T, Z = linalg.schur(A)
print T, Z
print Z.dot(T).dot(Z.T)[[1 3 2]
[1 4 5]
[2 3 6]]
[[ 9.90012467 1.78947961 -0.65498528]
[ 0. 0.54993766 -1.57754789]
[ 0. 0.51260928 0.54993766]] [[ 0.36702395 -0.85002495 -0.37782404]
[ 0.63681656 -0.06646488 0.76814522]
[ 0.67805463 0.52253231 -0.51691576]]
[[ 1. 3. 2.]
[ 1. 4. 5.]
[ 2. 3. 6.]]矩阵函数
考虑函数 $f(x)$ 的泰勒展开:
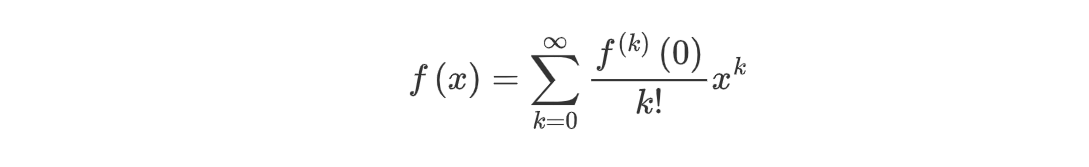
对于方阵,矩阵函数可以定义如下:

这也是计算矩阵函数的最好的方式。
指数和对数函数
指数
指数可以定义如下:
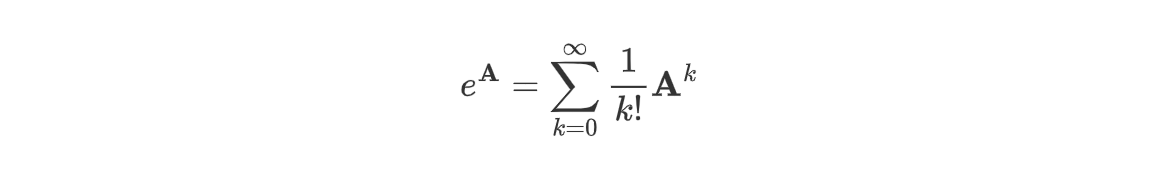
linalg.expm3 使用的是泰勒展开的方法计算结果:
A = np.array([[1, 2], [3, 4]])
print linalg.expm3(A)[[ 51.96890355 74.73648784]
[ 112.10473176 164.07363531]]另一种方法先计算 A 的特征值分解:
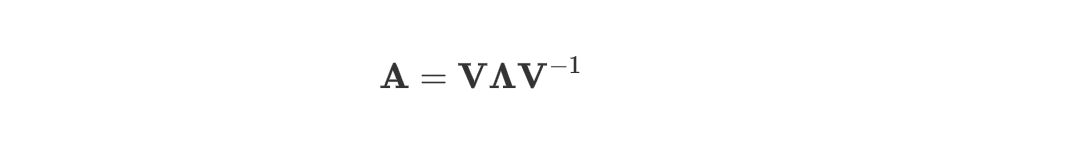
然后有(正交矩阵和对角阵的性质):
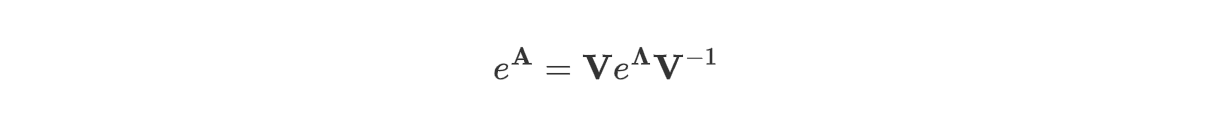
linalg.expm2 使用的就是这种方法:
print linalg.expm2(A)[[ 51.9689562 74.73656457]
[ 112.10484685 164.07380305]]最优的方法是用 Padé 近似 实现,Padé 近似往往比截断的泰勒级数准确,而且当泰勒级数不收敛时,Padé 近似往往仍可行,所以多用于在计算机数学中。
linalg.expm 使用的就是这种方法:
print linalg.expm(A)[[ 51.9689562 74.73656457]
[ 112.10484685 164.07380305]]对数
指数的逆运算,可以用 linalg.logm 实现:
print A
print linalg.logm(linalg.expm(A))[[1 2]
[3 4]]
[[ 1. 2.]
[ 3. 4.]]三角函数
根据欧拉公式,其定义为:
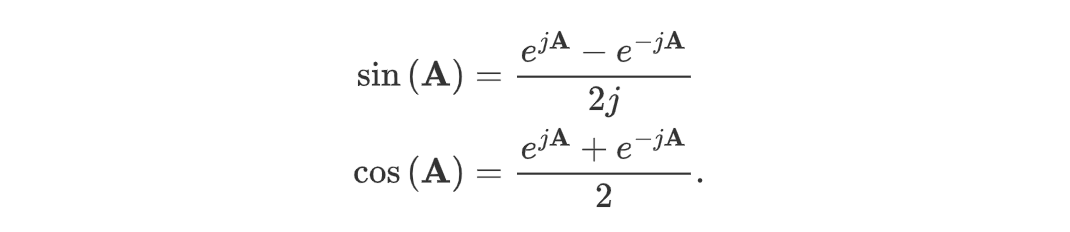
正切函数定义为:
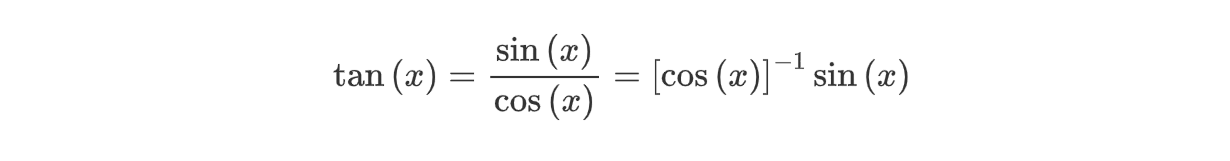
因此矩阵的正切函数定义为:

具体实现:
linalg.sinmlinalg.cosmlinalg.tanm
双曲三角函数
具体实现:
linalg.sinhmlinalg.coshmlinalg.tanhm
特殊矩阵
Scipy 提供了一些特殊矩阵的实现,具体可以参考:
http://docs.scipy.org/doc/scipy/reference/tutorial/linalg.html#special-matrices