Theano 循环:scan(详解)
import theano, time
import theano.tensor as T
import numpy as np
def floatX(X):
return np.asarray(X, dtype=theano.config.floatX)Using gpu device 1: Tesla C2075 (CNMeM is disabled)theano 中可以使用 scan 进行循环,常用的 map 和 reduce 操作都可以看成是 scan 的特例。
scan 通常作用在一个序列上,每次处理一个输入,并输出一个结果。
sum(x) 函数可以看成是 z + x(i) 函数在给定 z = 0 的情况下,对 x 的一个 scan。
通常我们可以将一个 for 循环表示成一个 scan 操作,其好处如下:
- 迭代次数成为符号图结构的一部分
- 最小化 GPU 数据传递
- 序列化梯度计算
- 速度比
for稍微快一些 - 降低内存使用
scan 的使用
函数的用法如下:
theano.scan(fn,
sequences=None,
outputs_info=None,
non_sequences=None,
n_steps=None,
truncate_gradient=-1,
go_backwards=False,
mode=None,
name=None,
profile=False,
allow_gc=None,
strict=False)主要参数的含义:
fn- 一步
scan所进行的操作
- 一步
sequences- 输入的序列
outputs_info- 前一步输出结果的初始状态
non_sequences- 非序列参数
n_steps- 迭代步数
go_backwards- 是否从后向前遍历
输出为一个元组 (outputs, updates):
outputs- 从初始状态开始,每一步
fn的输出结果
- 从初始状态开始,每一步
updates- 一个字典,用来记录
scan过程中用到的共享变量更新规则,构造函数的时候,如果需要更新共享变量,将这个变量当作updates的参数传入。
- 一个字典,用来记录
scan 和 map
这里实现一个简单的 map 操作,将向量 $\mathbf x$ 中的所有元素变成原来的两倍:
map(lambda t: t * 2, x)x = T.vector()
results, _ = theano.scan(fn = lambda t: t * 2,
sequences = x)
x_double_scan = theano.function([x], results)
print x_double_scan(range(10))[ 0. 2. 4. 6. 8. 10. 12. 14. 16. 18.]之前我们说到,theano 中的 map 是 scan 的一个特例,因此 theano.map 的用法其实跟 theano.scan 十分类似。
由于不需要考虑前一步的输出结果,所以 theano.map 的参数中没有 outputs_info 这一部分。
我们用 theano.map 实现相同的效果:
result, _ = theano.map(fn = lambda t: t * 2,
sequences = x)
x_double_map = theano.function([x], result)
print x_double_map(range(10))[ 0. 2. 4. 6. 8. 10. 12. 14. 16. 18.]scan 和 reduce
这里一个简单的 reduce 操作,求和:
reduce(lambda a, b: a + b, x)result, _ = theano.scan(fn = lambda t, v: t + v,
sequences = x,
outputs_info = floatX(0.))
# 因为每一步的输出值都会被记录到最后的 result 中,所以最后的和是 result 的最后一个元素。
x_sum_scan = theano.function([x], result[-1])
# 计算 1 + 2 + ... + 10
print x_sum_scan(range(10))45.0theano.reduce 也是 scan 的一个特例,使用 theano.reduce 实现相同的效果:
result, _ = theano.reduce(fn = lambda t, v: t + v,
sequences = x,
outputs_info = 0.)
x_sum_reduce = theano.function([x], result)
# 计算 1 + 2 + ... + 10
print x_sum_reduce(range(10))45.0reduce 与 scan 不同的地方在于,result 包含的内容并不是每次输出的结果,而是最后一次输出的结果。
scan 的使用
输入与输出
fn 是一个函数句柄,对于这个函数句柄,它每一步接受的参数是由 sequences, outputs_info, non_sequence 这三个参数所决定的,并且按照以下的顺序排列:
sequences中第一个序列的值- ...
sequences中最后一个序列的值outputs_info中第一个输出之前的值- ...
outputs_info中最后一个输出之前的值non_squences中的参数
这些序列的顺序与在参数 sequences, outputs_info 中指定的顺序相同。
默认情况下,在第 k 次迭代时,如果 sequences 和 outputs_info 中给定的值不是字典(dictionary)或者一个字典列表(list of dictionaries),那么
sequences中的序列seq传入fn的是seq[k]的值outputs_info中的序列output传入fn的是output[k-1]的值
fn 的返回值有两部分 (outputs_list, update_dictionary),第一部分将作为序列,传入 outputs 中,与 outputs_info 中的初始输入值的维度一致(如果没有给定 outputs_info ,输出值可以任意。)
第二部分则是更新规则的字典,告诉我们如何对 scan 中使用到的一些共享的变量进行更新:
return [y1_t, y2_t], {x:x+1}这两部分可以任意,即顺序既可以是 (outputs_list, update_dictionary), 也可以是 (update_dictionary, outputs_list),theano 会根据类型自动识别。
两部分只需要有一个存在即可,另一个可以为空。
例子分析
例如,在我们的第一个例子中
theano.scan(fn = lambda t: t * 2,
sequences = x)在第 k 次迭代的时候,传入参数 t 的值为 x[k]。
再如,在我们的第二个例子中:
theano.scan(fn = lambda t, v: t + v,
sequences = x,
outputs_info = floatX(0.))fn 接受了两个参数,初始迭代时,按照规则,t 接受的参数为 x[0],v 接受的参数为我们传入 outputs_info 的第一个初始值即 0 (认为是 outputs[-1]),他们的结果 t+v 将作为 outputs[0] 的值传入下一次迭代以及最终 scan 输出的 outputs 值中。
输入多个序列
我们可以一次输入多个序列,这些序列会按照顺序传入 fn 的参数中,例如计算多项式
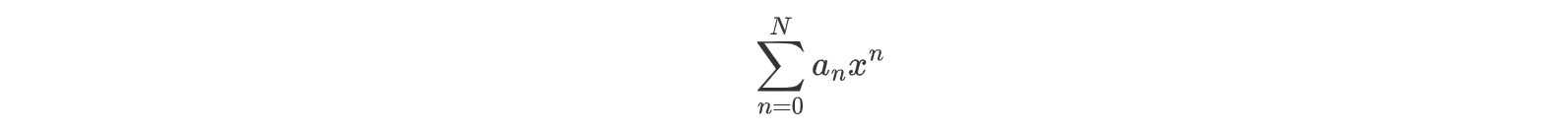
时,我们可以将多项式的系数和幂数两个序列放到一个 list 中作为输入参数:
# 变量 x
x = T.scalar("x")
# 不为 0 的系数
A = T.vectors("A")
# 对应的幂数
N = T.ivectors("N")
# a 对应的是 A, n 对应 N,v 对应 x
components, _ = theano.scan(fn = lambda a, n, v: a * (v ** n),
sequences = [A, N],
non_sequences = x)
result = components.sum()
polynomial = theano.function([x, A, N], result)
# 计算 1 + 3 * 10 ^ 2 + 2 * 10^3 = 2301
print polynomial(floatX(10),
floatX([1, 3, 2]),
[0, 2, 3])2301.0使用序列的多个值
默认情况下,我们只能使用输入序列的当前时刻的值,以及前一个输出的输出值。
事实上,theano 会将参数中的序列变成一个有 input 和 taps 两个键值的 dict:
input:输入的序列taps:要传入fn的值的列表- 对于
sequences参数中的序列来说,默认值为 [0],表示时间t传入t+0时刻的序列值,可以为正,可以为负。 - 对于
outputs_info参数中的序列来说,默认值为 [-1],表示时间t传入t-1时刻的序列值,只能为负值,如果值为None,表示这个输出结果不会作为参数传入fn中。
- 对于
传入 fn 的参数也会按照 taps 中的顺序来排列,我们考虑下面这个例子:
scan(fn, sequences = [ dict(input= Sequence1, taps = [-3,2,-1])
, Sequence2
, dict(input = Sequence3, taps = 3) ]
, outputs_info = [ dict(initial = Output1, taps = [-3,-5])
, dict(initial = Output2, taps = None)
, Output3 ]
, non_sequences = [ Argument1, Argument2])首先是 Sequence1 的 [-3, 2, -1] 被传入,然后 Sequence2 不是 dict, 所以传入默认值 [0],Sequence3 传入的参数是 3,所以 fn 在第 t 步接受的前几个参数是:
Sequence1[t-3]
Sequence1[t+2]
Sequence1[t-1]
Sequence2[t]
Sequence3[t+3]然后 Output1 传入的是 [-3, -5](传入的初始值的形状应为 shape (5,)+),Output2 不作为参数传入,Output3 传入的是 [-1],所以接下的参数是:
Output1[t-3]
Output1[t-5]
Output3[t-1]
Argument1
Argument2总的说来上面的例子中,fn 函数按照以下顺序最多接受这样 10 个参数:
Sequence1[t-3]
Sequence1[t+2]
Sequence1[t-1]
Sequence2[t]
Sequence3[t+3]
Output1[t-3]
Output1[t-5]
Output3[t-1]
Argument1
Argument2例子,假设 $x$ 是我们的输入,$y$ 是我们的输出,我们需要计算 $y(t) = tanh\left[W{1} y(t-1) + W{2} x(t) + W_{3} x(t-1)\right]$ 的值:
X = T.matrix("X")
Y = T.vector("y")
W_1 = T.matrix("W_1")
W_2 = T.matrix("W_2")
W_3 = T.matrix("W_3")
# W_yy 和 W_xy 作为不变的参数可以直接使用
results, _ = theano.scan(fn = lambda x, x_pre, y: T.tanh(T.dot(W_1, y) + T.dot(W_2, x) + T.dot(W_3, x_pre)),
# 0 对应 x,-1 对应 x_pre
sequences = dict(input=X, taps=[0, -1]),
outputs_info = Y)
Y_seq = theano.function(inputs = [X, Y, W_1, W_2, W_3],
outputs = results)测试小矩阵计算:
# 测试
t = 1001
x_dim = 10
y_dim = 20
x = 2 * floatX(np.random.random([t, x_dim])) - 1
y = 2 * floatX(np.zeros(y_dim)) - 1
w_1 = 2 * floatX(np.random.random([y_dim, y_dim])) - 1
w_2 = 2 * floatX(np.random.random([y_dim, x_dim])) - 1
w_3 = 2 * floatX(np.random.random([y_dim, x_dim])) - 1
tic = time.time()
y_res_theano = Y_seq(x, y, w_1, w_2, w_3)
print "theano running time {:.4f} s".format(time.time() - tic)
tic = time.time()
# 与 numpy 的结果进行比较:
y_res_numpy = np.zeros([t, y_dim])
y_res_numpy[0] = y
for i in range(1, t):
y_res_numpy[i] = np.tanh(w_1.dot(y_res_numpy[i-1]) + w_2.dot(x[i]) + w_3.dot(x[i-1]))
print "numpy running time {:.4f} s".format(time.time() - tic)
# 这里要从 1 开始,因为使用了 x(t-1),所以 scan 从第 1 个位置开始计算
print "the max difference of the first 10 results is", np.max(np.abs(y_res_theano[0:10] - y_res_numpy[1:11]))theano running time 0.0537 s
numpy running time 0.0197 s
the max difference of the first 10 results is 1.25780650354e-06测试大矩阵运算:
# 测试
t = 1001
x_dim = 100
y_dim = 200
x = 2 * floatX(np.random.random([t, x_dim])) - 1
y = 2 * floatX(np.zeros(y_dim)) - 1
w_1 = 2 * floatX(np.random.random([y_dim, y_dim])) - 1
w_2 = 2 * floatX(np.random.random([y_dim, x_dim])) - 1
w_3 = 2 * floatX(np.random.random([y_dim, x_dim])) - 1
tic = time.time()
y_res_theano = Y_seq(x, y, w_1, w_2, w_3)
print "theano running time {:.4f} s".format(time.time() - tic)
tic = time.time()
# 与 numpy 的结果进行比较:
y_res_numpy = np.zeros([t, y_dim])
y_res_numpy[0] = y
for i in range(1, t):
y_res_numpy[i] = np.tanh(w_1.dot(y_res_numpy[i-1]) + w_2.dot(x[i]) + w_3.dot(x[i-1]))
print "numpy running time {:.4f} s".format(time.time() - tic)
# 这里要从 1 开始,因为使用了 x(t-1),所以 scan 从第 1 个位置开始计算
print "the max difference of the first 10 results is", np.max(np.abs(y_res_theano[:10] - y_res_numpy[1:11]))theano running time 0.0754 s
numpy running time 0.1334 s
the max difference of the first 10 results is 0.000656997077348值得注意的是,由于 theano 和 numpy 在某些计算的实现上存在一定的差异,随着序列长度的增加,这些差异将被放大:
for i in xrange(20):
print "iter {:03d}, max diff:{:.6f}".format(i + 1,
np.max(np.abs(y_res_numpy[i + 1,:] - y_res_theano[i,:])))iter 001, max diff:0.000002
iter 002, max diff:0.000005
iter 003, max diff:0.000007
iter 004, max diff:0.000010
iter 005, max diff:0.000024
iter 006, max diff:0.000049
iter 007, max diff:0.000113
iter 008, max diff:0.000145
iter 009, max diff:0.000334
iter 010, max diff:0.000657
iter 011, max diff:0.001195
iter 012, max diff:0.002778
iter 013, max diff:0.004561
iter 014, max diff:0.004748
iter 015, max diff:0.014849
iter 016, max diff:0.012696
iter 017, max diff:0.043639
iter 018, max diff:0.046540
iter 019, max diff:0.083032
iter 020, max diff:0.123678控制循环次数
假设我们要计算方阵$A$的$A^k$,$k$ 是一个未知变量,我们可以这样通过 n_steps 参数来控制循环计算的次数:
A = T.matrix("A")
k = T.iscalar("k")
results, _ = theano.scan(fn = lambda P, A: P.dot(A),
# 初始值设为单位矩阵
outputs_info = T.eye(A.shape[0]),
# 乘 k 次
non_sequences = A,
n_steps = k)
A_k = theano.function(inputs = [A, k], outputs = results[-1])
test_a = floatX([[2, -2], [-1, 2]])
print A_k(test_a, 10)
# 使用 numpy 进行验证
a_k = np.eye(2)
for i in range(10):
a_k = a_k.dot(test_a)
print a_k[[ 107616. -152192.]
[ -76096. 107616.]]
[[ 107616. -152192.]
[ -76096. 107616.]]使用共享变量
可以在 scan 中使用并更新共享变量,例如,利用共享变量 n,我们可以实现这样一个迭代 k 步的简单计数器:
n = theano.shared(floatX(0))
k = T.iscalar("k")
# 这里 lambda 的返回值是一个 dict,因此这个值会被传入 updates 中
_, updates = theano.scan(fn = lambda n: {n:n+1},
non_sequences = n,
n_steps = k)
counter = theano.function(inputs = [k],
outputs = [],
updates = updates)
print n.get_value()
counter(10)
print n.get_value()
counter(10)
print n.get_value()0.0
10.0
20.0之前说到,fn 函数的返回值应该是 (outputs_list, update_dictionary) 或者 (update_dictionary, outputs_list) 或者两者之一。
这里 fn 函数返回的是一个字典,因此自动被放入了 update_dictionary 中,然后传入 function 的 updates 参数中进行迭代。
使用条件语句结束循环
我们可以将 scan 设计为 loop-until 的模式,具体方法是在 scan 中,将 fn 的返回值增加一个参数,使用 theano.scan_module 来设置停止条件。
假设我们要计算所有不小于某个值的 2 的幂,我们可以这样定义:
max_value = T.scalar()
results, _ = theano.scan(fn = lambda v_pre, max_v: (v_pre * 2, theano.scan_module.until(v_pre * 2 > max_v)),
outputs_info = T.constant(1.),
non_sequences = max_value,
n_steps = 1000)
# 注意,这里不能取 results 的全部
# 例如在输入值为 40 时,最后的输出可以看成 (64, False)
# scan 发现停止条件满足,停止循环,但是不影响 64 被输出到 results 中,因此要将 64 去掉
power_of_2 = theano.function(inputs = [max_value], outputs = results[:-1])
print power_of_2(40)[ 2. 4. 8. 16. 32.]