Theano 实例：人工神经网络

神经网络的模型可以参考 UFLDL 的教程，这里不做过多描述。

http://ufldl.stanford.edu/wiki/index.php/%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C

import theano
import theano.tensor as T
 
import numpy as np
from load import mnist

				

					
				
				

					
				
				

					
				
				

					
				
			

Using gpu device 1: Tesla K10.G2.8GB (CNMeM is disabled)

				

					
				
				

					
				
				

					
				
				

					
				
			

我们在这里使用一个简单的三层神经网络：输入 - 隐层 - 输出。

对于网络的激活函数，隐层用 sigmoid 函数，输出层用 softmax 函数，其模型如下：

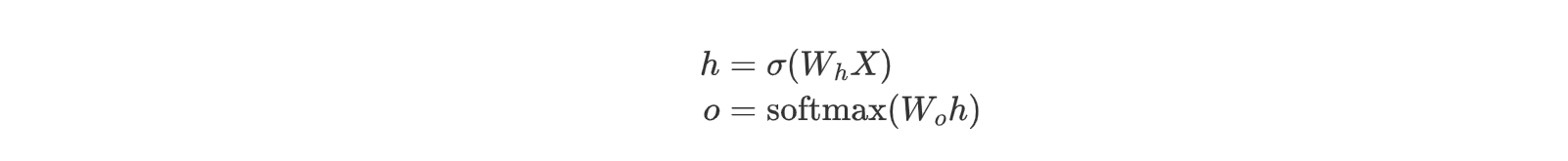
def model(X, w_h, w_o):
    """
    input:
        X: input data
        w_h: hidden unit weights
        w_o: output unit weights
    output:
        Y: probability of y given x
    """
    # 隐层
    h = T.nnet.sigmoid(T.dot(X, w_h))
    # 输出层
    pyx = T.nnet.softmax(T.dot(h, w_o))
    return pyx

				

					
				
				

					
				
				

					
				
				

					
				
			

使用随机梯度下降的方法进行训练：

def sgd(cost, params, lr=0.05):
    """
    input:
        cost: cost function
        params: parameters
        lr: learning rate
    output:
        update rules
    """
    grads = T.grad(cost=cost, wrt=params)
    updates = []
    for p, g in zip(params, grads):
        updates.append([p, p - g * lr])
    return updates

				

					
				
				

					
				
				

					
				
				

					
				
			

对于 MNIST 手写数字的问题，我们使用一个 784 × 625 × 10 即输入层大小为 784，隐层大小为 625，输出层大小为 10 的神经网络来模拟，最后的输出表示数字为 0 到 9 的概率。

为了对权重进行更新，我们需要将权重设为 shared 变量：

def floatX(X):
    return np.asarray(X, dtype=theano.config.floatX)
 
def init_weights(shape):
    return theano.shared(floatX(np.random.randn(*shape) * 0.01))

				

					
				
				

					
				
				

					
				
				

					
				
			

因此变量初始化为：

X = T.matrix()
Y = T.matrix()
 
w_h = init_weights((784, 625))
w_o = init_weights((625, 10))

				

					
				
				

					
				
				

					
				
				

					
				
			

模型输出为：

py_x = model(X, w_h, w_o)

				

					
				
				

					
				
				

					
				
				

					
				
			

预测的结果为：

y_x = T.argmax(py_x, axis=1)

				

					
				
				

					
				
				

					
				
				

					
				
			

模型的误差函数为：

cost = T.mean(T.nnet.categorical_crossentropy(py_x, Y))

				

					
				
				

					
				
				

					
				
				

					
				
			

更新规则为：

updates = sgd(cost, [w_h, w_o])

				

					
				
				

					
				
				

					
				
				

					
				
			

定义训练和预测的函数：

train = theano.function(inputs=[X, Y], outputs=cost, updates=updates, allow_input_downcast=True)
predict = theano.function(inputs=[X], outputs=y_x, allow_input_downcast=True)

				

					
				
				

					
				
				

					
				
				

					
				
			

训练：

导入 MNIST 数据：

trX, teX, trY, teY = mnist(onehot=True)

				

					
				
				

					
				
				

					
				
				

					
				
			

训练 100 轮，正确率为 0.956：

for i in range(100):
    for start, end in zip(range(0, len(trX), 128), range(128, len(trX), 128)):
        cost = train(trX[start:end], trY[start:end])
    print "{0:03d}".format(i), np.mean(np.argmax(teY, axis=1) == predict(teX))

				

					
				
				

					
				
				

					
				
				

					
				
			

000 0.7028
001 0.8285
002 0.8673
003 0.883
004 0.89
005 0.895
006 0.8984
007 0.9017
008 0.9047
009 0.907
010 0.9089
011 0.9105
012 0.9127
013 0.914
014 0.9152
015 0.9159
016 0.9169
017 0.9173
018 0.918
019 0.9185
020 0.919
021 0.9197
022 0.9201
023 0.9205
024 0.9206
025 0.9212
026 0.9219
027 0.9228
028 0.9228
029 0.9229
030 0.9236
031 0.9244
032 0.925
033 0.9255
034 0.9263
035 0.927
036 0.9274
037 0.9278
038 0.928
039 0.9284
040 0.9289
041 0.9294
042 0.9298
043 0.9302
044 0.9311
045 0.932
046 0.9325
047 0.9332
048 0.934
049 0.9347
050 0.9354
051 0.9358
052 0.9365
053 0.9372
054 0.9377
055 0.9385
056 0.9395
057 0.9399
058 0.9405
059 0.9411
060 0.9416
061 0.9422
062 0.9427
063 0.9429
064 0.9431
065 0.9438
066 0.9444
067 0.9446
068 0.9449
069 0.9453
070 0.9458
071 0.9462
072 0.9469
073 0.9475
074 0.9474
075 0.9476
076 0.948
077 0.949
078 0.9497
079 0.95
080 0.9503
081 0.9507
082 0.9507
083 0.9515
084 0.9519
085 0.9521
086 0.9523
087 0.9529
088 0.9536
089 0.9538
090 0.9542
091 0.9545
092 0.9544
093 0.9546
094 0.9547
095 0.9549
096 0.9552
097 0.9554
098 0.9557
099 0.9562