Theano 基础
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt首先导入 theano 及其 tensor 子模块(tensor,张量):
import theano
# 一般都把 `tensor` 子模块导入并命名为 T
import theano.tensor as TUsing gpu device 1: Tesla K10.G2.8GB (CNMeM is disabled)tensor 模块包含很多我们常用的数学操作,所以为了方便,将其命名为 T。
符号计算
theano 中,所有的算法都是用符号计算的,所以某种程度上,用 theano 写算法更像是写数学(之前在[04.06 积分](../04. scipy/04.06 integration in python.ipynb)一节中接触过用 sympy 定义的符号变量)。
用 T.scalar 来定义一个符号标量:
foo = T.scalar('x')print foox支持符号计算:
bar = foo ** 2
print barElemwise{pow,no_inplace}.0这里定义 foo 是 $x$,bar 就是变量 $x^2$,但显示出来的却是看不懂的东西。
为了更好的显示 bar,我们使用 theano.pp() 函数(pretty print)来显示:
print theano.pp(bar)(x ** TensorConstant{2})查看类型:
print type(foo)
print foo.type
TensorType(float32, scalar) theano 函数
有了符号变量,自然可以用符号变量来定义函数,theano.function() 函数用来生成符号函数:
theano.function(input, output)其中 input 对应的是作为参数的符号变量组成的列表,output 对应的是输出,输出可以是一个,也可以是多个符号变量组成的列表。
例如,我们用刚才生成的 foo 和 bar 来定义函数:
square = theano.function([foo], bar)使用 square 函数:
print square(3)9.0也可以使用 bar 的 eval 方法,将 x 替换为想要的值,eval 接受一个字典作为参数,键值对表示符号变量及其对应的值:
print bar.eval({foo: 3})9.0theano.tensor
除了 T.scalar() 标量之外,Theano 中还有很多符号变量类型,这些都包含在 tensor(张量)子模块中,而且 tensor 中也有很多函数对它们进行操作。
T.scalar(name=None, dtype=config.floatX)- 标量,shape - ()
T.vector(name=None, dtype=config.floatX)- 向量,shape - (?,)
T.matrix(name=None, dtype=config.floatX)- 矩阵,shape - (?,?)
T.row(name=None, dtype=config.floatX)- 行向量,shape - (1,?)
T.col(name=None, dtype=config.floatX)- 列向量,shape - (?,1)
T.tensor3(name=None, dtype=config.floatX)- 3 维张量,shape - (?,?,?)
T.tensor4(name=None, dtype=config.floatX)- 4 维张量,shape - (?,?,?,?)
shape 中为 1 的维度支持 broadcast 机制。
除了直接指定符号变量的类型(默认 floatX),还可以直接在每类前面加上一个字母来定义不同的类型:
bint8wint16iint32lint64dfloat64ffloat32ccomplex64zcomplex128
例如 T.dvector() 表示的就是一个 float64 型的向量。
除此之外,还可以用它们的复数形式一次定义多个符号变量:
x,y,z = T.vectors('x','y','z')
x,y,z = T.vectors(3)A = T.matrix('A')
x = T.vector('x')
b = T.vector('b')T.dot() 表示矩阵乘法:
$$y = Ax+b$$
y = T.dot(A, x) + bMARKDOWN_HASH3eb1fc0ae926386d7326332406756d49MARKDOWNHASH 表示进行求和:
$$z = \sum{i,j} A_{ij}^2$$
z = T.sum(A**2)来定义一个线性函数,以 $A,x,b$ 为参数,以 $y,z$ 为输出:
linear_mix = theano.function([A, x, b],
[y, z])使用这个函数:
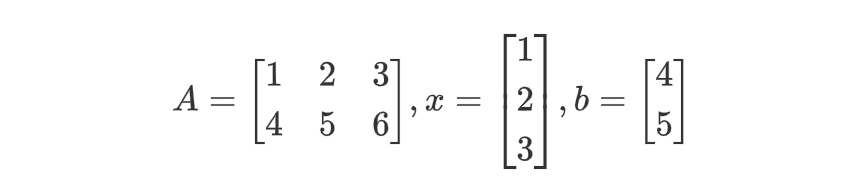
print linear_mix(np.array([[1, 2, 3],
[4, 5, 6]], dtype=theano.config.floatX), #A
np.array([1, 2, 3], dtype=theano.config.floatX), #x
np.array([4, 5], dtype=theano.config.floatX)) #b[array([ 18., 37.], dtype=float32), array(91.0, dtype=float32)]这里 dtype=theano.config.floatX 是为了与 theano 设置的浮点数精度保持一致,默认是 float64,但是在 GPU 上一般使用 float32 会更高效一些。
我们还可以像定义普通函数一样,给 theano 函数提供默认值,需要使用 theano.Param 类:
linear_mix_default = theano.function([A, x, theano.Param(b, default=np.zeros(2, dtype=theano.config.floatX))],
[y, z])计算默认参数下的结果:
print linear_mix_default(np.array([[1, 2, 3],
[4, 5, 6]], dtype=theano.config.floatX), #A
np.array([1, 2, 3], dtype=theano.config.floatX)) #x[array([ 14., 32.], dtype=float32), array(91.0, dtype=float32)]计算刚才的结果:
print linear_mix_default(np.array([[1, 2, 3],
[4, 5, 6]], dtype=theano.config.floatX), #A
np.array([1, 2, 3], dtype=theano.config.floatX), #x
np.array([4, 5], dtype=theano.config.floatX)) #b[array([ 18., 37.], dtype=float32), array(91.0, dtype=float32)]共享的变量
Theano 中可以定义共享的变量,它们可以在多个函数中被共享,共享变量类似于普通函数定义时候使用的全局变量,同时加上了 global 的属性以便在函数中修改这个全局变量的值。
shared_var = theano.shared(np.array([[1.0, 2.0], [3.0, 4.0]], dtype=theano.config.floatX))
print shared_var.typeCudaNdarrayType(float32, matrix)可以通过 set_value 方法改变它的值:
shared_var.set_value(np.array([[3.0, 4], [2, 1]], dtype=theano.config.floatX))通过 get_value() 方法返回它的值:
print shared_var.get_value()[[ 3. 4.]
[ 2. 1.]]共享变量进行运算:
shared_square = shared_var ** 2
f = theano.function([], shared_square)
print f()[[ 9. 16.]
[ 4. 1.]]这里函数不需要参数,因为共享变量隐式地被认为是一个参数。
得到的结果会随这个共享变量的变化而变化:
shared_var.set_value(np.array([[1.0, 2], [3, 4]], dtype=theano.config.floatX))
print f()[[ 1. 4.]
[ 9. 16.]]一个共享变量的值可以用 updates 关键词在 theano 函数中被更新:
subtract = T.matrix('subtract')
f_update = theano.function([subtract], shared_var, updates={shared_var: shared_var - subtract})这个函数先返回当前的值,然后将当前值更新为原来的值减去参数:
print 'before update:'
print shared_var.get_value()
print 'the return value:'
print f_update(np.array([[1.0, 1], [1, 1]], dtype=theano.config.floatX))
print 'after update:'
print shared_var.get_value()before update:
[[ 1. 2.]
[ 3. 4.]]
the return value:
after update:
[[ 0. 1.]
[ 2. 3.]] 导数
Theano 的一大好处在于它对符号变量计算导数的能力。
我们用 T.grad() 来计算导数,之前我们定义了 foo 和 bar (分别是 $x$ 和 $x^2$),我们来计算 bar 关于 foo 的导数(应该是 $2x$):
bar_grad = T.grad(bar, foo) # 表示 bar (x^2) 关于 foo (x) 的导数
print bar_grad.eval({foo: 10})20.0再如,对之前的 $y = Ax + b$ 求 $y$ 关于 $x$ 的雅可比矩阵(应当是 $A$):
y_J = theano.gradient.jacobian(y, x)
print y_J.eval({A: np.array([[9.0, 8, 7], [4, 5, 6]], dtype=theano.config.floatX), #A
x: np.array([1.0, 2, 3], dtype=theano.config.floatX), #x
b: np.array([4.0, 5], dtype=theano.config.floatX)}) #b[[ 9. 8. 7.]
[ 4. 5. 6.]]theano.gradient.jacobian 用来计算雅可比矩阵,而 theano.gradient.hessian 可以用来计算 Hessian 矩阵。
R-op 和 L-op
Rop 用来计算 $\frac{\partial f}{\partial x}v$,Lop 用来计算 $v\frac{\partial f}{\partial x}$:
一个是雅可比矩阵与列向量的乘积,另一个是行向量与雅可比矩阵的乘积。
W = T.dmatrix('W')
V = T.dmatrix('V')
x = T.dvector('x')
y = T.dot(x, W)
JV = T.Rop(y, W, V)
f = theano.function([W, V, x], JV)
print f([[1, 1], [1, 1]], [[2, 2], [2, 2]], [0,1])[ 2. 2.]