本文最后更新于 704 天前,其中的信息可能已经过时,如有错误请发送邮件到wuxianglongblog@163.com
不要迷信默认设置
导入相关的包:
import numpy as np
import matplotlib.pyplot as plt生成三角函数:
x = np.linspace(-np.pi, np.pi)
c, s = np.cos(x), np.sin(x)默认绘图
%matplotlib inline
# 画图
p = plt.plot(x,c)
p = plt.plot(x,s)
# 在脚本中需要加上这句才会显示图像
plt.show()
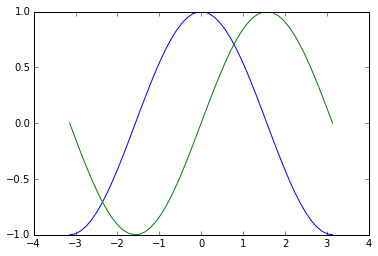
默认效果如图所示,我们可以修改默认的属性来得到更漂亮的结果。
图
图像以 Figure # 为窗口标题,并且数字从 1 开始,figure() 函数的主要参数如下:
| 参数 | 默认值 | 描述 |
|---|---|---|
num |
1 |
图号 |
figsize |
figure.figsize |
图大小(宽,高)(单位英寸) |
dpi |
figure.dpi |
分辨率(每英寸所打印的点数) |
facecolor |
figure.facecolor |
背景颜色 |
edgecolor |
figure.edgecolor |
边界颜色 |
frameon |
True |
是否显示图框架 |
# 设置图像大小
f = plt.figure(figsize=(10,6), dpi=80)
# 画图
p = plt.plot(x,c)
p = plt.plot(x,s)
# 在脚本中需要加上这句才会显示图像
plt.show()设置线条颜色,粗细,类型
首先,我们使用 figure() 函数来创建一幅新图像,并且指定它的大小,使得长宽比更合适。
然后,我们使用 color, linewidth, linestyle 参数,指定曲线的颜色,粗细,类型:
# 设置图像大小
f = plt.figure(figsize=(10,6), dpi=80)
# 画图,指定颜色,线宽,类型
p = plt.plot(x, c, color="blue", linewidth=2.5, linestyle="-")
p = plt.plot(x, s, color="red", linewidth=2.5, linestyle="-")
# 在脚本中需要加上这句才会显示图像
# plt.show()
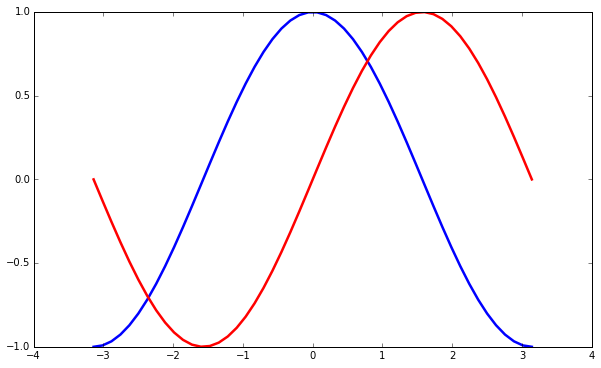
也可以像 Matlab 中一样使用格式字符来修改参数:
表示颜色的字符参数有:
| 字符 | 颜色 |
|---|---|
‘b’ |
蓝色,blue |
‘g’ |
绿色,green |
‘r’ |
红色,red |
‘c’ |
青色,cyan |
‘m’ |
品红,magenta |
‘y’ |
黄色,yellow |
‘k’ |
黑色,black |
‘w’ |
白色,white |
表示类型的字符参数有:
| 字符 | 类型 | 字符 | 类型 |
|---|---|---|---|
'-' |
实线 | '--' |
虚线 |
'-.' |
虚点线 | ':' |
点线 |
'.' |
点 | ',' |
像素点 |
'o' |
圆点 | 'v' |
下三角点 |
'^' |
上三角点 | '<' |
左三角点 |
'>' |
右三角点 | '1' |
下三叉点 |
'2' |
上三叉点 | '3' |
左三叉点 |
'4' |
右三叉点 | 's' |
正方点 |
'p' |
五角点 | '*' |
星形点 |
'h' |
六边形点1 | 'H' |
六边形点2 |
'+' |
加号点 | 'x' |
乘号点 |
'D' |
实心菱形点 | 'd' |
瘦菱形点 |
'_' |
横线点 |
# 设置图像大小
f = plt.figure(figsize=(10,6), dpi=80)
# 画图,指定颜色,线宽,类型
p = plt.plot(x, c, 'b-',
x, s, 'r-', linewidth=2.5)
# 在脚本中需要加上这句才会显示图像
# plt.show()

设置横轴纵轴的显示区域
我们希望将坐标轴的显示区域放大一些,这样可以看到所有的点,可以使用 plt 中的 xlim 和 ylim 来设置:
# 设置图像大小
p = plt.figure(figsize=(10,6), dpi=80)
# 画图,指定颜色,线宽,类型
p = plt.plot(x, c, 'b-',
x, s, 'r-', linewidth=2.5)
########################################################################
# 设置显示范围
p = plt.xlim(x.min() * 1.1, x.max() * 1.1)
p = plt.ylim(c.min() * 1.1, c.max() * 1.1)
########################################################################
# 在脚本中需要加上这句才会显示图像
# plt.show()
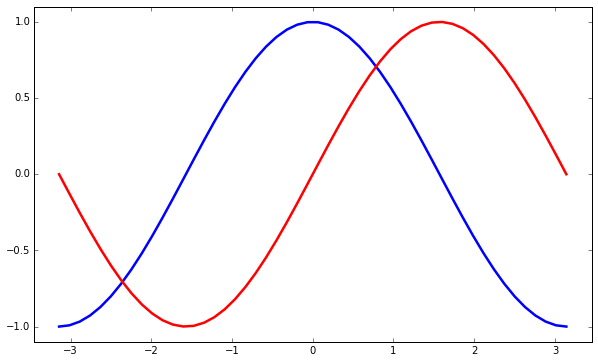
设置刻度
对于三教函数来说,我们希望将 x 轴的刻度设为与 $\pi$ 有关的点,可以使用 plt 中的 xticks 和 yticks 函数,将需要的刻度传入:
# 设置图像大小
f = plt.figure(figsize=(10,6), dpi=80)
# 画图,指定颜色,线宽,类型
p = plt.plot(x, c, 'b-',
x, s, 'r-', linewidth=2.5)
# 设置显示范围
plt.xlim(x.min() * 1.1, x.max() * 1.1)
plt.ylim(c.min() * 1.1, c.max() * 1.1)
###########################################################################
# 设置刻度
p = plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi])
p = plt.yticks([-1, 0, 1])
###########################################################################
# 在脚本中需要加上这句才会显示图像
# plt.show()
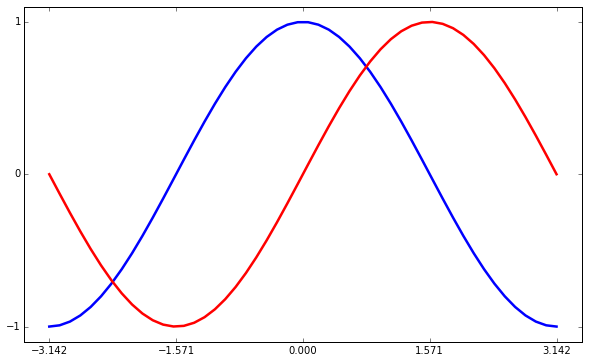
设定 x 轴 y 轴标题
我们想让刻度的位置显示的是含有 $\pi$ 的标识而不是浮点数,可以在 xticks 中传入第二组参数,这组参数代表对应刻度的显示标识。这里,我们使用 latex 的语法来显示特殊符号(使用 $$ 包围的部分):
# 设置图像大小
f = plt.figure(figsize=(10,6), dpi=80)
# 画图,指定颜色,线宽,类型
p = plt.plot(x, c, 'b-',
x, s, 'r-', linewidth=2.5)
# 设置显示范围
plt.xlim(x.min() * 1.1, x.max() * 1.1)
plt.ylim(c.min() * 1.1, c.max() * 1.1)
# 设置刻度及其标识
p = plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
['$-\pi$', '$-\pi/2$', '$0$', '$\pi/2$', '$\pi$'], fontsize ='xx-large')
p = plt.yticks([-1, 0, 1],
['$-1$', '$0$', '$+1$'], fontsize ='xx-large')
# 在脚本中需要加上这句才会显示图像
# plt.show()
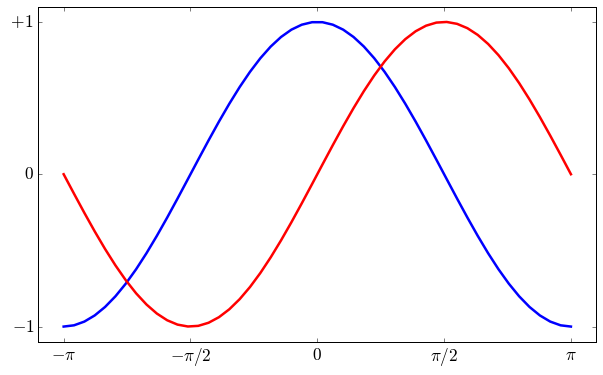
移动坐标轴的位置
现在坐标轴的位置是在边界上,而且有上下左右四条,我们现在想将下面和左边的两条移动到中间,并将右边和上面的两条去掉:
# 设置图像大小
f = plt.figure(figsize=(10,6), dpi=80)
# 画图,指定颜色,线宽,类型
plt.plot(x, c, 'b-',
x, s, 'r-', linewidth=2.5)
# 设置显示范围
plt.xlim(x.min() * 1.1, x.max() * 1.1)
plt.ylim(c.min() * 1.1, c.max() * 1.1)
# 得到轴的句柄
ax = plt.gca()
# ax.spines参数表示四个坐标轴线
# 将右边和上边的颜色设为透明
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
###################################################################################
# 将 x 轴的刻度设置在下面的坐标轴上
ax.xaxis.set_ticks_position('bottom')
# 设置位置
ax.spines['bottom'].set_position(('data',0))
# 将 y 轴的刻度设置在左边的坐标轴上
ax.yaxis.set_ticks_position('left')
# 设置位置
ax.spines['left'].set_position(('data',0))
###################################################################################
# 设置刻度及其标识
p = plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
['$-\pi$', '$-\pi/2$', '$0$', '$\pi/2$', '$\pi$'], fontsize ='xx-large')
p = plt.yticks([-1, 0, 1],
['$-1$', '$0$', '$+1$'], fontsize ='xx-large')
# 在脚本中需要加上这句才会显示图像
# plt.show()
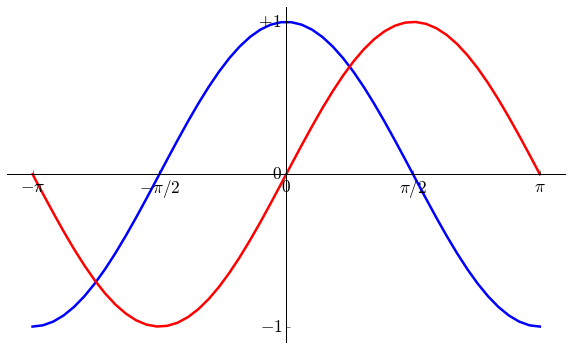
加入图例
使用 legend() 加入图例:
# 设置图像大小
plt.figure(figsize=(10,6), dpi=80)
# 画图,指定颜色,线宽,类型
plt.plot(x, c, 'b-',
x, s, 'r-', linewidth=2.5)
# 设置显示范围
plt.xlim(x.min() * 1.1, x.max() * 1.1)
plt.ylim(c.min() * 1.1, c.max() * 1.1)
# 得到画图的句柄
ax = plt.gca()
# ax.spines参数表示四个坐标轴线
# 将右边和上边的颜色设为透明
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
# 将 x 轴的刻度设置在下面的坐标轴上
ax.xaxis.set_ticks_position('bottom')
# 设置位置
ax.spines['bottom'].set_position(('data',0))
# 将 y 轴的刻度设置在左边的坐标轴上
ax.yaxis.set_ticks_position('left')
# 设置位置
ax.spines['left'].set_position(('data',0))
# 设置刻度及其标识
plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
['$-\pi$', '$-\pi/2$', '$0$', '$\pi/2$', '$\pi$'], fontsize ='xx-large')
plt.yticks([-1, 0, 1],
['$-1$', '$0$', '$+1$'], fontsize ='xx-large')
##################################################################################################
# 加入图例,frameon表示去掉图例周围的边框
l = plt.legend(['cosine', 'sine'], loc='upper left', frameon=False)
##################################################################################################
# 在脚本中需要加上这句才会显示图像
# plt.show()
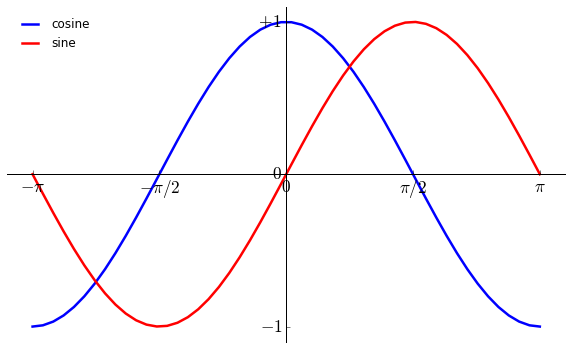
注释特殊点
我们可以使用 annotate 函数来注释特殊的点,假设我们要显示的点是 $2\pi/3$:
# 设置图像大小
plt.figure(figsize=(10,6), dpi=80)
# 画图,指定颜色,线宽,类型
plt.plot(x, c, 'b-',
x, s, 'r-', linewidth=2.5)
# 设置显示范围
plt.xlim(x.min() * 1.1, x.max() * 1.1)
plt.ylim(c.min() * 1.1, c.max() * 1.1)
# 得到画图的句柄
ax = plt.gca()
# ax.spines参数表示四个坐标轴线
# 将右边和上边的颜色设为透明
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
# 将 x 轴的刻度设置在下面的坐标轴上
ax.xaxis.set_ticks_position('bottom')
# 设置位置
ax.spines['bottom'].set_position(('data',0))
# 将 y 轴的刻度设置在左边的坐标轴上
ax.yaxis.set_ticks_position('left')
# 设置位置
ax.spines['left'].set_position(('data',0))
# 设置刻度及其标识
plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
['$-\pi$', '$-\pi/2$', '$0$', '$\pi/2$', '$\pi$'], fontsize ='xx-large')
plt.yticks([-1, 0, 1],
['$-1$', '$0$', '$+1$'], fontsize ='xx-large')
# 加入图例,frameon表示图例周围是否需要边框
l = plt.legend(['cosine', 'sine'], loc='upper left', frameon=False)
####################################################################################
# 数据点
t = 2 * np.pi / 3
# 蓝色虚线
plt.plot([t,t],[0,np.cos(t)], color ='blue', linewidth=2.5, linestyle="--")
# 该点处的 cos 值
plt.scatter([t,],[np.cos(t),], 50, color ='blue')
# 在对应的点显示文本
plt.annotate(r'$\sin(\frac{2\pi}{3})=\frac{\sqrt{3}}{2}$', # 文本
xy=(t, np.sin(t)), # 数据点坐标位置
xycoords='data', # 坐标相对于数据
xytext=(+10, +30), # 文本位置坐标
textcoords='offset points', # 坐标相对于数据点的坐标
fontsize=16, # 文本大小
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2")) # 箭头
# 红色虚线
p = plt.plot([t,t],[0,np.sin(t)], color ='red', linewidth=2.5, linestyle="--")
# 该点处的 sin 值
p = plt.scatter([t,],[np.sin(t),], 50, color ='red')
# 显示文本
p = plt.annotate(r'$\cos(\frac{2\pi}{3})=-\frac{1}{2}$',
xy=(t, np.cos(t)), xycoords='data',
xytext=(-90, -50), textcoords='offset points', fontsize=16,
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
#####################################################################################
# 在脚本中需要加上这句才会显示图像
# plt.show()
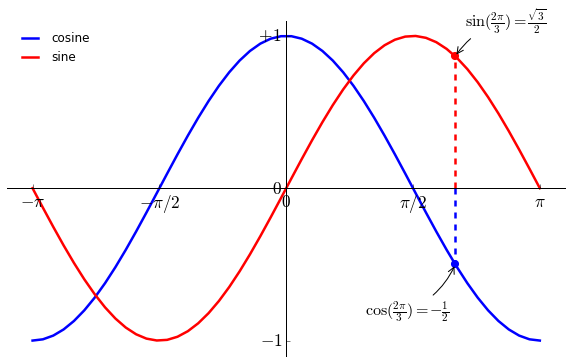
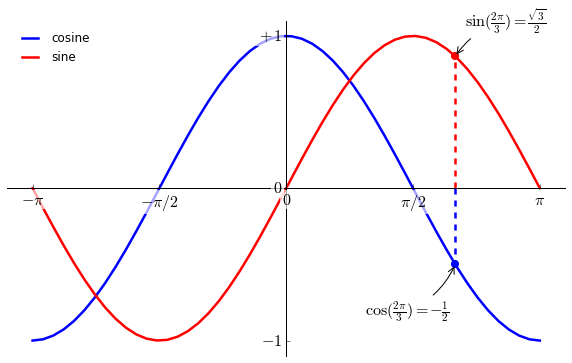
最后调整
调整刻度值的大小,并让其显示在曲线上方。
# 设置图像大小
plt.figure(figsize=(10,6), dpi=80)
# 画图,指定颜色,线宽,类型
plt.plot(x, c, 'b-',
x, s, 'r-', linewidth=2.5)
# 设置显示范围
plt.xlim(x.min() * 1.1, x.max() * 1.1)
plt.ylim(c.min() * 1.1, c.max() * 1.1)
# 得到画图的句柄
ax = plt.gca()
# ax.spines参数表示四个坐标轴线
# 将右边和上边的颜色设为透明
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
# 将 x 轴的刻度设置在下面的坐标轴上
ax.xaxis.set_ticks_position('bottom')
# 设置位置
ax.spines['bottom'].set_position(('data',0))
# 将 y 轴的刻度设置在左边的坐标轴上
ax.yaxis.set_ticks_position('left')
# 设置位置
ax.spines['left'].set_position(('data',0))
# 设置刻度及其标识
plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
['$-\pi$', '$-\pi/2$', '$0$', '$\pi/2$', '$\pi$'], fontsize ='xx-large')
plt.yticks([-1, 0, 1],
['$-1$', '$0$', '$+1$'], fontsize ='xx-large')
# 加入图例,frameon表示图例周围是否需要边框
l = plt.legend(['cosine', 'sine'], loc='upper left', frameon=False)
# 数据点
t = 2 * np.pi / 3
# 蓝色虚线
plt.plot([t,t],[0,np.cos(t)], color ='blue', linewidth=2.5, linestyle="--")
# 该点处的 cos 值
plt.scatter([t,],[np.cos(t),], 50, color ='blue')
# 在对应的点显示文本
plt.annotate(r'$\sin(\frac{2\pi}{3})=\frac{\sqrt{3}}{2}$', # 文本
xy=(t, np.sin(t)), # 数据点坐标位置
xycoords='data', # 坐标相对于数据
xytext=(+10, +30), # 文本位置坐标
textcoords='offset points', # 坐标相对于数据点的坐标
fontsize=16, # 文本大小
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2")) # 箭头
# 红色虚线
p = plt.plot([t,t],[0,np.sin(t)], color ='red', linewidth=2.5, linestyle="--")
# 该点处的 sin 值
p = plt.scatter([t,],[np.sin(t),], 50, color ='red')
# 显示文本
p = plt.annotate(r'$\cos(\frac{2\pi}{3})=-\frac{1}{2}$',
xy=(t, np.cos(t)), xycoords='data',
xytext=(-90, -50), textcoords='offset points', fontsize=16,
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
#####################################################################################
for label in ax.get_xticklabels() + ax.get_yticklabels():
label.set_fontsize(16)
label.set_bbox(dict(facecolor='white', edgecolor='None', alpha=0.65 ))
####################################################################################
# 在脚本中需要加上这句才会显示图像
# plt.show()
The devil is in the details.